-
\(\triangleright\) Définition: suites adjacentes
Soient \((U_n)_{n\in N}\) et \(V_n\) 2 suites réelles. On dit que \(U_n\) et \(V_n\) sont adjacentes si:- \(U_n\) est croissante et \(V_n\) est décroissante
- \(\forall n\in \Bbb N, U_n\leq V_n\)
- \(\underset{n\longrightarrow\infty}\lim (U_n-V_n)=0\)
\(\triangleright\) Théorème:
Deux suites adjacentes convergent vers la même limite.
\(\longrightarrow\) preuve:
\(\forall n\in \Bbb N\) on a:
\(U_n\leq V_n\leq V_n+1\) (par hypothèse, \(V_n\) décroissante et \(U_n\leq V_n\))
Donc \((U_n)_{n\in N}\) est croissante et majorée par \(V_0\)
Par le théorème de convergence monotone, \((U_n)_{n\in N}\) converge vers \(l\).
De plus, on a : \(V_n= U_n+(V_n-U_n)\)
Comme \(U_n \longrightarrow l\) et \(\lim(V_n-U_n)=0\)
Le théorème sur les opérations de limites implique que \(V_n\) est convergente et \(\lim (V_n) =\lim (U_n)+\lim (V_n-U_n)\)
Donc \(\lim V_n=l\)
\(\triangleright\) Théorème de Bolzano Weierstrass:
\(\longrightarrow\)Toute suite bornée réelle admet une sous-suite convergente.
>\(\longrightarrow\)
preuve: (par dichotomie)
Soit \(U_n\) une suite bornée.
\(\exists a,b\in \Bbb R\) telle que \(\forall n\in \Bbb N, a\leq U_n\leq b\)
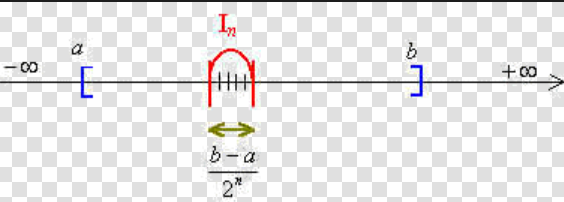Il existe (au moins) un des deux intevalles \([a; \frac{a+b}{2}]\)
On a \([\frac{a+b}{2};b]\) qui contient une infinité de termes.
Disons \([a,\frac{a+b}{2}]\) et \(\exists \phi(1)\gt \phi(0)\) tel que \(U_{\phi(1)}=[a_1,b_1]\) et \(b_1-a_1=\frac{b-a}{2}\)
Puis on recommence. Il existe deux suites \(A_n\) et \(B_n\) telles que \(A_n\) croissante et \(B_n\) décroissante.
\(A_n\leq B_n, \forall n\in N\)
\(B_n-A_n=\frac{b-a}{2^n}\)
Et \(\exists \phi:N\) associe \(N\) corissante tel que \(U_{\phi(n)}\in [A_n, B_n]\)
\(A_n\) et \(B_n\) sont adjacentes donc converge vers l.
\(A_n\leq U_{\phi(n)}\leq B_n\) \(\implies\) \(\lim U_{\phi(n)}=l\)
